今回、この本を読んでみました。

気になった方は著書自体に戻って数式のエッセンスを追っていくとなお理解が深まります。

 序章

「ITと数学の素晴らしき結婚」によって、人工知能やディープラーニングが生まれた話の前段です。

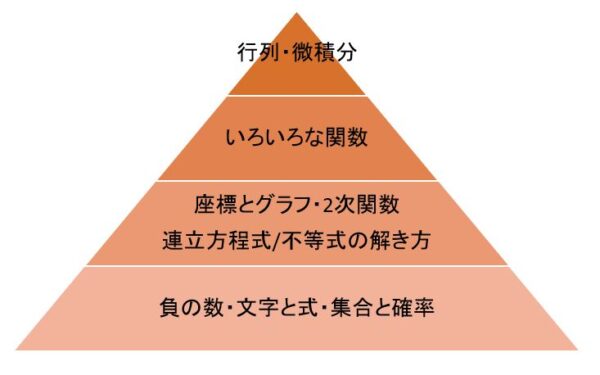
微積分を頂点とした数学が現在の数学の主流となっております。これを再編成して、機械学習を学ぶための数学として再編して届けています。つまり、再編の段階で、幾何学の分野を大胆にカットしています。

レベルとして、足し算・引き算・掛け算・割り算とちょっとした図形の知識で追えるように説明しています。

図示もしてくれています。

1章：入門編

四則演算から始まる

四則演算から話が始まります。数学のアレルギーがない人であれば、読み飛ばしてもいいです。基礎的な数の扱い方を学び、機械学習で出てくる数式のアレルギーを減らす導入です。

とても丁寧に説明をしてくれる内容なので、数学が苦手な人が一から始めるのにとても分かりやすいです。数学の始まりでつまずく人がいる、マイナスの考え方や、割り算は「分数の掛け算」といった点もしっかりと解説してくれています。

記号論理学の世界

代数学の話の次に、ベン図や記号論理学の話を説明してくれています。機械学習の中で出てくる証明内の論理展開に慣れるための話です。

証明したいことがら（ここでは命題と呼んでいます）を証明するには、下記の4つが上げられます。

1. 証明したい命題と「同値」な命題が真であることを示す
2. 証明したい命題を「包含」する命題が真であることを示す
3. 証明したい命題の「対偶」が真であることを示す
4. 証明したい命題が「偽」だとすると矛盾が生じることを示す

証明したい事柄のために、どのように事柄を示していけばいいかに慣れる章です。

基本的な確率計算とベイズ統計学の考え方

確率について説明をしてくれます。機械学習の根幹の根幹で出てくる確率の計算について説明をしてくれます。

また、たまに話に出てくるベイズ統計学についても触れております。

ベイズ統計は条件付き確率の応用のようなもので、ここではエントリーシートに「やる気」と書いていいる学生が「優秀」である確率を考える例を示してくれています。

 第2章：二次関数

二次関数を総合的に学んでいきます。機械学習やディープラーニングでもっと複雑な関数を現実モデルとする基礎になります。基礎なので二次関数を基礎からさらってくれています。

基本的な一次関数の説明と訪問件数→営業成績のモデル作成

二次関数の基本的な説明から入ります。分かる方はこの点は飛ばせます

連立方程式の例題が出てきますが、この中で営業訪問数の例題があります。

営業訪問を増やせば直線的なペースで契約数も増えるとした場合、彼は来年100件の契約を取るためにいったい何回の営業訪問をしなければいけないと推測されるだろうか？（P095）

営業は足で稼ぐから考えずに訪問しろと言われている人もいるかもしれません。ここではそういった非論理性は排除して、成果を出すための行動を考えるきっかけを来れます。
（「直線的なペース」と断りがあるのは、実際は訪問数を増やしても質が下がる頭打ちがあるからです。「直線的」でないものは後ほどイメージ付してくれます）

ここでは基本的なモデルの考察を教えてくれます。

連立不等式での領域制限と二次関数モデル

例題は$$業務システムを受ける件数=x$$と$$スマートフォンアプリ受注する件数=y$$とした場合の売上を最大化する割合です。

エンジニアは業務システムを1件こなすには5ヶ月、アプリは1ヶ月かかります。デザイナーは業務システムに2ヶ月、アプリに4ヶ月かかるとすると、下記の連立方程式の解が最大化するためのバランスとなります。

$$x=5x+y\leq12$$

$$x=2x+4y\leq12$$

現実世界でもよく例題としてあがる内容ではないでしょうか。

二次関数でのモデル例

訪問数と成果は直線モデルで比例しないことは、営業経験者なら明らかに分かるでしょう。正確なモデルに近づける考察のために、二次関数モデルを考えます。次のような形です。

$$y=a+bx+cx^2(abcは定数)$$

ここで、3年間のデータを元に、abcをここで仮に決定します。書籍内では下記の数式を提示してくれています。

$$y=-8+12x+6x^2(abcは定数)$$

最適な値を探すのは、関数を分析するため

最適な値を探す方法として平方完成を示してくれています。ただ、ここは眺める程度でいいです。数学が苦手な人は平方完成する前に本を閉じます。

コンピュータを使うと考えるなら、平方完成は概念を抑えておけば十分です。

なぜ関数を分析する必要があるか

機械学習や統計学では、（A)「モデル」を考えます。

モデルが（B)「現実の実測値」とどれだけ合っているかを考えます。

数学的には、（A)と（B)との差を取りその差の合計が一番小さくなるところ＝（A)「モデル」が一番正しいもの。そういう決め方をしていきます。

このために最適な値を見つける必要が出てくるのです。

第3章：二項定理、対数、三角関数

二項定理は「あることが起こるか起こらないか」のモデル化ができる

二項定理の説明は3次関数や4次関数の係数と絡めて説明をしてくれています。

ただ、「あることが起こるか起こらないか」というものをモデル化するためにもっと力を発揮します。

モデル化はビジネスマンが理解しやすいものを提示してくれています。

ある若き営業マンが100回訪問すると3~4回成約をとってくる若き営業マン（以前の分析で成約の確率は36%）が、10回訪問したのにたった2回しか成約を取ってこなかった。

上司はあまり気にするなとアドバイスをくれたが、このアドバイスは正しいのかただの気休めか？

（P172から要約）

こういったケースもよくありますね。10回訪問して成約を取る確率計算として、二項分布を使って具体的な計算をしてくれています。内容は本書にゆずるとして、結果としては24%程度は10回に2回しか成約がとれないケースがこの営業マンの場合あると結論付けています。

対数の役立ち

対数の説明に入っていきます。対数は、計算を簡便にするのに役立ちます。

天文学などでとてつもなく大きな値を扱う際に、10を底とする対数表を使うことで計算を楽にした歴史を示してくれています。

$$90日間は何秒か？＝90ｘ24ｘ60ｘ60＝6^5\times10^3$$

対数はネイピア数を底とするのはなぜか

ネイピア数を底とすると微分しやすいからです。

ネイピア数はヤコブ・ベルヌーイが考え出し、レオンハルト・オイラーがその性質を研究したということだそうです。

ネイピア数は$$e=2.71828…$$

複利の計算が例題としてあがっているように、時間軸と兼ね合わせた事象にもよく使えます。

ロジスティック回析の例示

ロジスティック回析の例示をしてくれています。ロジスティック回帰は機械学習で言えば、シグモイド関数を使った単純パーセプトロンと呼ばれます。

三平方の定理でデータの距離＝ズレの距離を考える

データは座標軸で考えます。そのズレを考えるのに三平方の定理を使っていきます。

その他微分への用意として、三角関数入門と弧度法での角度表現を説明してくれています。弧度法を使う理由は、以下の2つです。

• 微積分がしやすいから
• マイナスの値で場合分けをしなくてよいから

第4章　ベクトル・Σ

Σ（シグマ）について

Σ（シグマ）はたくさんの値をまとめて書きたいためにあります。

「データをたくさん用意して、それを最初から最後まで足したい」と表現するのに、

$$\sum_{k=1}^{n} a_{k} = a_{1} + a_{2} + \dots + a_{n}$$

ベクトルの内積とΣ（シグマ）の関係

ベクトルの内積は次のように表せます。これはΣを使った内容と同じです。

$$\vec{a} \cdot \vec{b} = a_1 b_1 + a_2 b_2 + a_3 b_3=\sum_{k=1}^{n} a_{k} b_{k}$$

ベクトルの内積としてΣの合計を表現できることで、なおのこと簡単に多くのデータを表現することができます。

Σの合計がベクトルにつながるのはこの点からです。

統計学でのベクトルの内積

統計学や機械学習はでは同じものをかけ合わせて合計するというのがよく出てきます。

それ故にベクトルの内積で考えると楽ということになるのです((P289))。

行列はベクトルよりデータ数が多いときに便利

もっとたくさんのデータを扱いたいときは行列を使うと楽です。

この後は行列の四則演算・転地・正方行列の説明をしてくれます。

第5章　統計学と機械学習のための微分・積分

微分と機械学習

微分は「ちょうどいいところを探す」ために役に立ちます。

統計学や機械学習のためということで、分からない人のために微分の基本的なやり方から説明をしてくれています。

積分と機械学習

積分は、関数の値を集めて「面」や「立体」を考えるために使います。そんなことが必要なのは、「確率密度関数」を理解するためです。

例題を見ると分かりやすいでしょう。

あるエンジニアが上司から作業時間の見積が甘いと叱られた。数学的根拠とともに「バッファ込みでこれだけの期間があれば95%大丈夫」という数字を見積もれと指示を受けた。

この確率を理解するものが確率密度関数です。

確率密度関数は複雑な関数になります。その関数の面積はその事象が起こる確率です。よってその面積を使いたいということになります。そこで積分が使われます。

最尤法（さいゆうほう）が微積を学ぶ最も大きな意味

最尤法（さいゆうほう）というのは、データに最もあてはまりの良いパラメーターを探す方法です。

ここで出てくる関数は100や1000の関数の掛け算になっています。計算を簡便にするために、対数をとって掛け算を足し算化します。

対数をとったものを対数尤度といい、これが最大になるところを探していきます。

統計学と機械学習の定石です。

Π（大文字パイ）の説明

ちなみに、Σ（シグマ）の掛け算版がでてきます。

\\\Pi（パイ）\\

となっており、全てをかけ合わせたものです。

第6章　ディープラーニング

偏微分は、複数の変数のうち一つだけに着目した微分

偏微分の説明から始まっています。

偏微分は、複数の変数があった際に一つの変数がちょっと増えた場合に傾きがどうなるかという内容です。

通常の文字の偏微分に加えて、行列表記での偏微分の説明もあります。コンピュータの力技として数式を組み立てるために役に立ちます。

そして、ニューラルネットワークの説明が続いています。ニューラルネットワークは、「人間の脳を模した謎のテクノロジー」などではなく、単に「変な関数の良い近似方法」(P508)だという説明がされています。

まとめ

全体として、面白い記述が多かったです。ページ数548あります。丁寧な記述が追っかけやすいので、興味がある人はぜひ購入してください。

【編集後記】
万全の良い内容でなくても形にして出していく。そういうつもりでブログに書いていきます。加筆訂正ご指摘あればぜひ教えてください。

【昨日のはじめて】
mathjax
surface1の再インストール

【子どもと昨日】
手放しで立てるようになってきました。膝にもたれかかった後で、パッと私の膝を放してみる。そんな動作をします。「自分でたってみた」という感じで立つ感じでしょうか。時間をかけてゆっくり挑戦してほしいです。

参考図書の付録

さてその後の参考文献一覧もとても役に立ちます。参考書籍のオススメの理由も本書に丁寧に書いてありますので、今後の学習をしたい方も下記書籍を参考にしてみてください。

統計学を勉強したい場合

因果推論を学びたいなら

 重回帰分析やロジスティック解析、一般化線形モデルについては

MCMC法とかも分かるような内容になっています。

心理統計学や軽量心理学で一般線形かモデルでない手法

項目反応理論とか、アンケートのその裏側にある概念を測定しようとする場合

同様の著者でR学ぶなら

もっと専門的なものは

• 項目反応理論[入門編][理論編]

情報取得