数学オリンピックの問題を解きました。補助線の引き方で、見えないものが見えるようになります。抽象化した問題ですが、仕事へのアプローチにも使えます。
数学オリンピックの問題
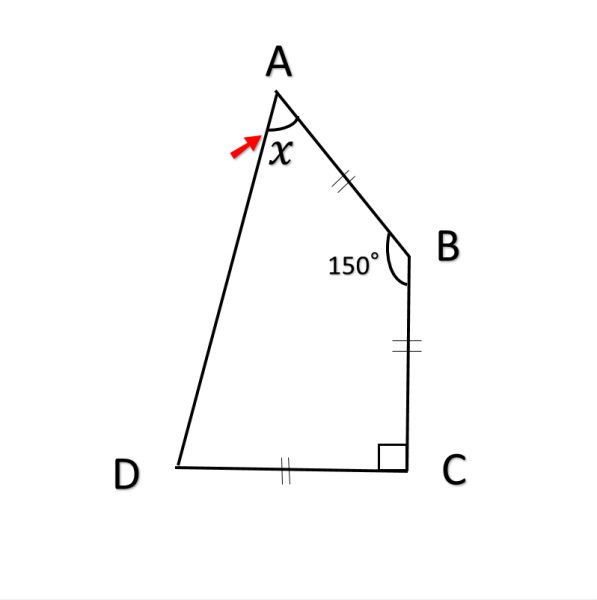
問題は、AB=BC=CDであり、∠ABC=150°、BCD=90°の条件で、
∠DABを求めます。
比較的簡単に解けそうな問題です。しかし、補助線の入れかたが思いつかないとなかなか最後まではも止まりません。
解き方
まずは、正方形を書きます。
正方形を書くと、BC=CD=DD’=D’B(=AB)となります。
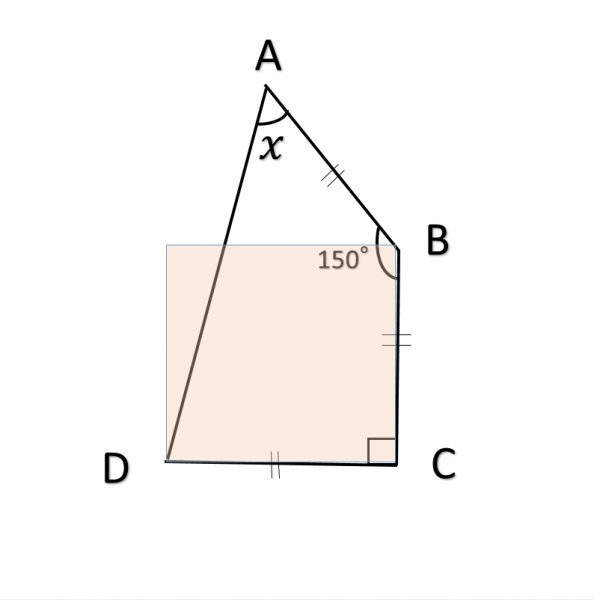
正方形を書いた後に、角Aとその正方形のD’を結びます。
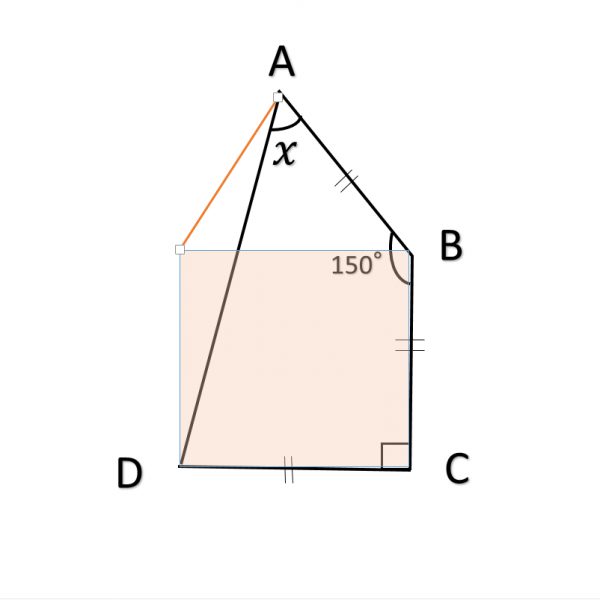
正三角形ができるので、
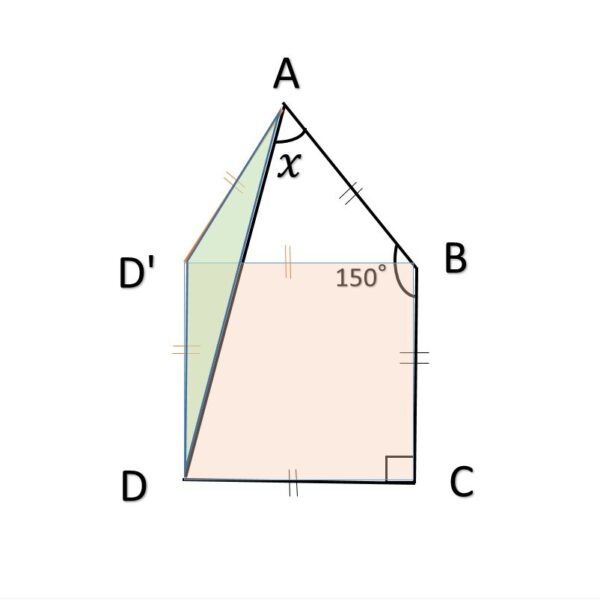
・∠D’ABが正三角形になるので、どの角も60°になります。また、∠DD’Aは、正三角形の角(60°)と正方形の角(90°)を足した150°となります。
・∠DD’Aは二等辺三角形のため、∠D’AD=15°となります。
x=∠D’ABー∠D’AD=60°ー15°=45° となります。
仕事への応用として

答えを見てしまうと、補助線さえ引ければ簡単に感じますよね。
実際の仕事においても複雑そうに見えることは、このような補助線を引いて考えるイメージをすることで、簡単に解けることがあります。解決方法をいくつか考えてみる際の参考にしてみてください。
【編集後記】
久々に図形問題に取り組むとなかなか冷や汗をかきますよね。取り組む楽しさというのは、いつも感じます。
【昨日のはじめて】
エクセルマクロを使った解決案を二つ作って1日で運用にこぎつけました。急ぐと少々荒いところが出るので、デバックは慎重にしないとですね。
【昨日 子どもと】
早起きして一緒に過ごしました。何時でもかわいいです。
